On Strassen's algorithm for matrix multiplication

 This article is a short description of the Strassen’s algorithm for matrix multiplication.

Thinking of multiplying the two matrices A and B, and as a result there is a matrix C. Then we can say:

C = AB

Plus, I encountered with the following formula:

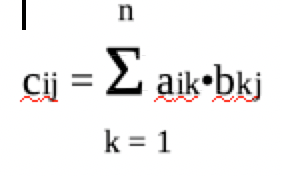
I confess that I’m dorky that at the first glance it was hard for me to grasp what this means. Then often the difficulty of understanding comes from our misinterpretation of the premises.

Our high school math class taught us, in order to multiply vector A and B, you need to focus on the specific row of the matrix A, and if the row size is n, then the row size of B must be n as well. Then, you need to multiply and add it up one by one.

The important thing here is the i and j in the above formula is fixed value.

Given the n (maximum column size of A) as 5 (because giving the actual fixed value can make it easier to understand),

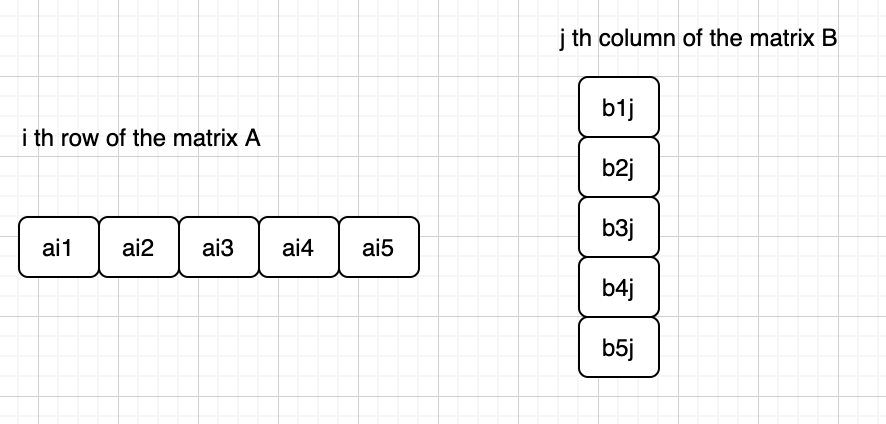
then

ai1 • b1j + ai2 • b2j +ai3 • b3j +ai4 • b4j +ai5 • b5j = cij

So programmatically, Strassen’s algorithm is described as:

This might take Θ(n³) (maybe… correct me if i’m wrong)

Presumably I wasted your time just walking through the high school math thing, but just wanted to clarify this Strassen’s part.

Thanks for the reading.